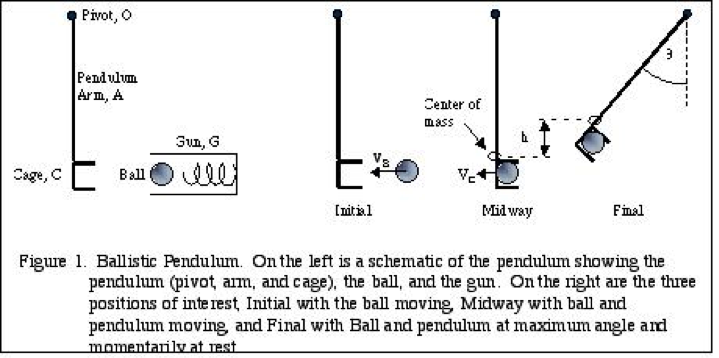
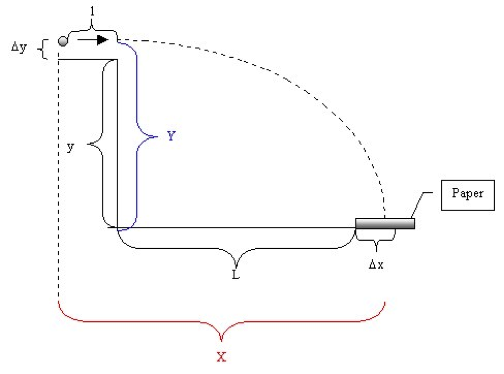
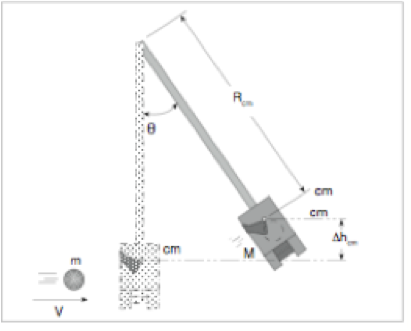
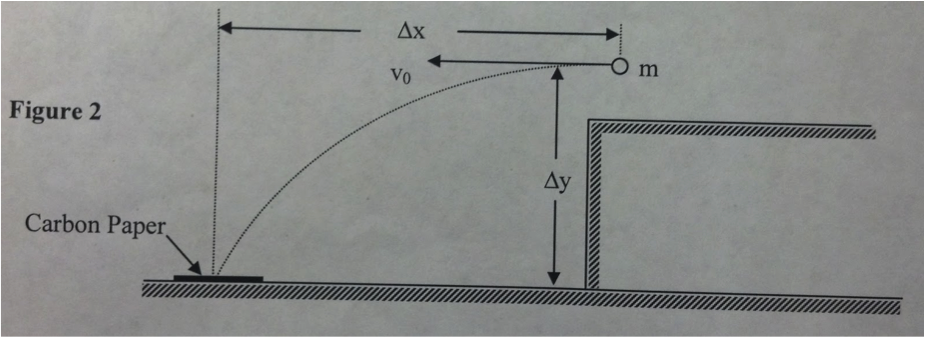
Ballistic Pendulum Experiment
Written by Arturo
I. ABSTRACT
For experiment 13 Ballistic Pendulum, we used the conservation of momentum and mechanical energy to determine the velocity of a ball as it is shot from a launcher. The angle was measured every time the launcher was released for method A. For method B, we removed the pendulum bob and shot the ball off the table onto the floor, where we recorded the distance of the x axis from the table to the spot where the ball landed.
II. THEORY
In Method A, the experiment test that one can determine the ball’s velocity by shooting a ball into a pendulum bob and then analyzing the bob’s motion using the principles of conservation of momentum and conservation of mechanical energy. In Method B, the projectile motion of the ball is studied to determine its initial velocity.
Applying conservation of momentum, we have mVA = (m+ M)Vf just before and after the ball contacted the bob, where m is the mass of the ball and M is the mass of the bob, and VA and VB are the ball’s speed just before and just after collision. As they contacted each other, the potential energy that they both have at the highest swing are equal, giving us the equation, .5(m+M)Vf2 = (m+M)*gh. This equation can be further broken down into mVA = (m+M)(2gh)0.5. Solving for VA, we end up getting (m+M)/m * (2gh)0.5.
For the vertical motion of the ball we have the equation Y = 0.5gt2, where down is positive, t is the time of flight, and g is the acceleration due to gravity. We solve for the time and get t = (2Y/g)0.5. The horizontal component of the velocity is constant and equal to the initial velocity VB, making X = VB t. We then solve for VB = x * (g/2Y)0.5
III.PROCEDURE
The experiment was begun by loading the ball into the launcher to the medium setting. We then made sure that the stopper was at the 0 degree reading. After we check the stopper we fired the ball into the pendulum bob. After we fired the ball we recorded the angle corresponding to the highest point reached by the pendulum bob. We repeated this part of the experiment several times and recorded the degree each time.
When we were done this Method A, we moved onto Method B. We began Method B by removing the pendulum bob and shooting the ball onto the floor. We did this about five times and measured the vertical and horizontal directions every time, recording the data after.
IV. DATA
Method A
| Trial | 1 | 2 | 3 | 4 | 5 |
| x° | 27.0° | 29.5° | 27.0° | 27.5° | 27.0° |
(L)Length of arm of shooter = 0.300 m (m)mass of ball = 0.66 kg (M)mass of bob = 0.242 kg
Method B
| Trial | 1 | 2 | 3 | 4 | 5 |
| X m | 1.357 m | 1.373 m | 1.367 m | 1.382 m | 1.368 m |
(Y)-axis distance = 0.831 m
V. CALCULATIONS
- Method A
x° average = added degrees = 27.0°+29.5°+27.0°+27.5°+27.0° = 27.6°
total 5
Height =L(1-cos(°)) = 0300(1-cos(27.6))
KEbefore = .5mvi2 =.5(0.66)(3.815)2 = 0.479 J
KEafter = .5(m + M)Vf2 = .5(0.66+0.242)(0.8175)2 = 0.103 J
KEafter/KEbefore = 0.103/ 0.479 = 0.215
Ball’s initial velocity Va = (m+M)/m * (2gh)0.5 = ((0.66+0.240)/0.066) * (2(9.8)(0.0341))0.5
Uncertainties for:
Mass of ball= 0.00005kg mass of bob= 0.00005kg length of arm shooter= 0.0005m degree= 0.05°= 8.73×10-4 rad
δ Height= H * ((δL /L)2 + ((sin° * δ°)/(1-cos°))2).5 =
= 0.0341 * ((0.0005/0.300)2 + ((sin0.482) * 8.73×10-4)/ (1-cos(0.482)))2).5
= 0.00708
δVA = VA * ((δM/ m+M)2 + ((M * δm)/(m(m+M)))2 + (δH/ 2H)2 + (δg/ 2g)2)0.5
δVA = 3.815 *((0.00005/0.0001)2 + ((0.242 * 0.00005)/((0.066)(0.066+0.242)))2 + (0.00708/2(0.0341))2 + (0.1/2(9.8))2
δVA = 0.51
2. Method B
x average = total distances = 1.357 m +1.373 m +1.367 m +1.382 m +1.368 m= 1.369 m
total 5
VB = X * (g/2Y)0.5 = 1.369 * (9.8/2(0.831))0.5 = 3.32 m/s
δx = 0.0005 δY = 0.0005
δVB = VB * ((δX/ 2X)2 (δY/ 2Y)2 + (δg/ 2g)2)0.5 = 0.49
VI. CONCLUSION
We performed this experiment to analyze how velocity is directly related to the conservation of momentum and mechanical energy. We concluded that if the initial velocity of the ball in Method B were to double to a stronger launcher spring, the ball’s time of flight would stay relatively the same because the vertical acceleration and vertical velocity are still the same. We also came up with that what had happened to the “lost” kinetic energy of the ball was that the energy got transformed into other types of energy such as thermal energy and sound energy. The conclusion of the experiment proved that the momentum in collision is equal to the initial momentum. One way in which the accuracy of this data could be improved is by maybe trying to have the trials on the floor. This would help because the tables are not sturdy, so they can be moved by the slightest touch. This can cause the degree reader to appear higher or lower than it really was. Another way we can improve the accuracy of the measurements is by having equipment that is more precise and advanced. As far as the results go, they were pretty much on point, with a 0.34 deviance for the ball’s initial velocity of 3.815 m/s in Method A.
VII. REFERENCES