Analyzing a Hydrogen Storage Material
By: Jaime Rodriguez
Background:
With hydrogen technology research reaching an all-time high, several different materials to store this element have been analyzed. Palladium is a hydrogen storage material under heavy consideration, due to the fact that it can absorb immense amounts of hydrogen. Although practical, one disadvantage is that it is indeed a precious metal, thus it is expensive. Also, as hydrogen is absorbed it spreads the existing palladium particles apart and therefore certain compounds will stick to the surface. Heating the palladium prior to hydrogen absorption is performed in order to minimize this affect, but it takes money to provide heat, and again cost is a factor.
Palladium is not the only hydrogen storage material. Two promising materials currently being researched are lithium borohydride and sodium borohydride. Both these materials are applied in the same manner as palladium. One disadvantage that these two materials have over palladium is that they form weaker bonds, thus resulting in less energy needed to release the stored hydrogen. (Hydrogen Storage Materials). These materials do have their own disadvantages of course. For instance, if these bonds that were just mentioned end up being too weak, the pressure required to rehydride the material is too high, and would thereby eliminate any energy savings from the release of the hydrogen. (Hydrogen Storage Materials).
It is clear that there is still much more research to be done before hydrogen storage can be made commercially practical. Progress is being made every day.
Procedure:
No changes were made to the procedure of the experiment. It was followed just as it was written.
Data and Results:
Table 1:
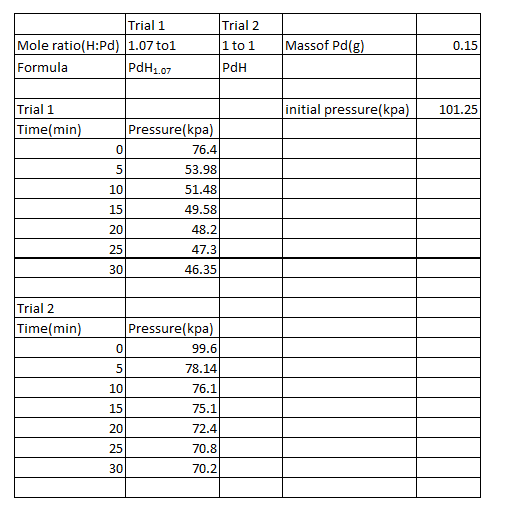
The following are sample calculations for trial 1.

The non-stoichiometric formulas were as PdH1.07 and PdH for trials 1 and 2, respectively. Of the two trials, the maximum amount of hydrogen absorbed by the palladium was in trial 1. It absorbed .6042L of hydrogen. This value of course is not possible as only .6L of hydrogen was utilized. The amount of hydrogen absorbed should have been less than 70%. This signifies that there were numerous amounts of experimental error, mostly systematic intrinsic error and random error due to measurement. One systematic intrinsic error may have been the transfer of the syringe from the hydrogen tank to the LabQuest. Much of the hydrogen could have been lost in the process. Also, there could have been systematic error in the manner that the pressure in the syringe was adjusted at each time a measurement was recorded.
The volume of the palladium piece was found by taking the density(12.02g/cm^3), inversing it, and then multiplying it by the mass, which was .15g. Putting into consideration that 1cm^3 is equal to 1L, the volume of the palladium was .012L. Thus, the ratio of hydrogen absorbed to the metal is 50.35:1, which of course is not accurate due to the experimental errors
In order to find how much water a sponge with a volume of 225cm^3 must absorb to match this ratio, it must be multiplied by the ratio of hydrogen absorbed, 50.35L. This would result in the sponge absorbing 11,328.75L of water. This clearly shows how ludicrous the results of the experiment came to be.
Reflection:
The experiment itself was tricky and certainly prone to numerous amounts of experimental error. It is unclear how to really make any significant improvements to the procedure, as this process is not relatively simple. With that being said, the experiment was performed to the best of our abilities. An annoying aspect was the amount of time needed to wait to while collecting data.
References:
Hydrogen Storage Materials. (n.d.).sigmaaldrich.com. Retrieved April 2, 2013, from http://www.sigmaaldrich.com/etc/medialib/docs/Aldrich/Brochure/al_material_matters_v2n2.Par.0001.File.tmp/al_material_matters_v2n2.pdf
