Detecting Art Forgeries
Introduction
The use of differential models is important in many different aspects of life. In our particular case we used a differential model to aid us in the detection of art forgeries. By using the known properties of radioactive decay and techniques involving differential equations, we were able to determine the dates that paintings were created. We used these techniques to determine the authenticity of several paintings claiming to be the original works of Eugene Delacroix and Jan Vermeer. We then provided our opinions, based on the confidence intervals of dates, towards the validity of the paintings up for auction.
Body
Elements of high atomic weight are generally unstable and decay spontaneously; this attribute is known as radioactivity. In some cases these radioactive elements decay into different elements. This decay is proportional to the amount of substance present. A model of decay can be represented simply by the differential equation:
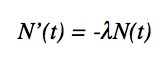
Where N’(t) is the change in amount over a time, λ is the positve decay constant, and N(t) is the amount present. Given the initial condition N(to) = No, an equation for the amount of substance at any time t was found to be:

Knowing that the half-life of lead-210 is twenty two years, we concluded that at t= 22 years, N(t) = ½ No. Substituting this N(t) into previously derived formula you can calculate the value of lambda to be:
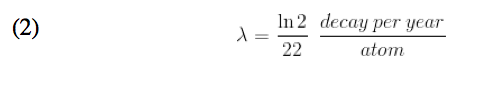
Now, knowing the value of our decay constant we devised another differential equation to model the decay of lead-210 proportional to the amount of lead-210 present and the decay rate of radium-226 at any time t:
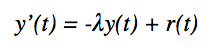
By knowing that the half life of Radium-226 is 1600 years we made the assumption that r(t) is constant over the time period of 150 to 350 years. We made this assumption when we derived the decay constant of the radium. When we made this derivation it was found that:

Where decay constant k of this differential equation is:

As you can see the very small value of k leads to a relatively constant value of r(t) for the 150 to 350 year period that we assumed it to be constant. Having proven this to be true, we let , we now know both the decay rate of polonium-210 and radium-266 per minute per gram. However, even though we know both the decay rates we are still not able to calculate the age of the paintings without knowing the initial amount of the two elements.
By noting the value of the decay constants and the relationship between the initial amount of radium and polonium:

If you know the initial amount of radium you can find the initial amount of the polonium using the formula:
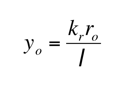
Using this formula and the initial value of radium you can solve the initial differential equation, y(t), where t is the time now, you can set up a definite integral over the life span of the painting to find the present amount of polonium. Because we used a definite integral from the time the painting was painted to the present time, and can measure the amount of polonium in the paint we were able to solve for the year the painting was painted. This process can by expressed in the formula:
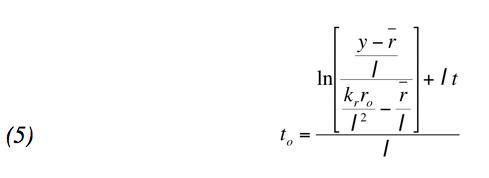
We then employed the technique of a separation factor (the initial value of polonium over the decay of radium) to compute the dates of the paintings. Making some assumption of the separation factors i.e. the SF of Lacemaker and The Death of Sardanapla is 100, we can determine the year the paintings were painted. The process of finding the initial amount of polonium is simple:
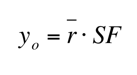
Inserting this value into and then substituting it into the equation we solved for the initial date the painting was made. We then used this method to determine whether or not the paintings are forgeries. However, since we’re making assumptions for the separation factors of each of the paintings we cannot assume our calculated dates are exact.
To compute a more exact range of dates, we used known separation factors of various paintings to make 50% and 95% confidence intervals. For the 50% interval our separation factors range from [33,208]. For the 95% interval our separation factors range from [5.8,1192]. Using the range of separation factors we computed a range of dates that we are sure that paintings must have been painted in. Using these intervals we determined whether or not the paintings were forgeries.
Conclusion
Through our knowledge of differential models and decay rates we were able to create a formula to determine the time of creation of a painting. We employed this formula to the information of the decays of radium-226 and polonium-210 in the paintings to find a range of years in which the paintings could have been made:
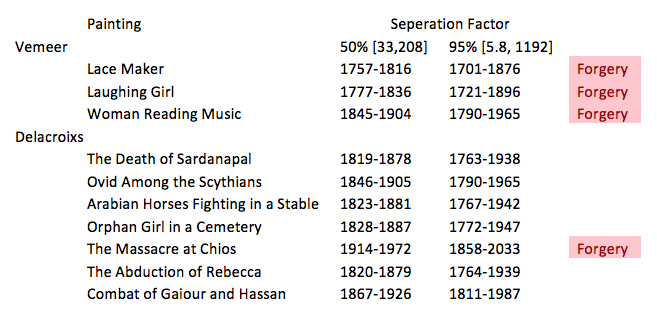
As shown in this table, we can make the recommendation to Christie that the three Vemeer paintings are not authentic and that The Massacre at Chios is also a forgery.
