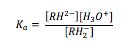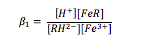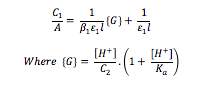Determination of the stability constant for an iron (iii) sulfosalicylate complex
Written by Dan
Abstract
The stoichiometry of the major complex formed was determined to have a 1:1 ratio of iron (iii) and sulfosalicylate acid using the continuous variation method. The stability constant for the formation of the complex was then calculated using spectroscopic analysis and pH measurements to be 420.45 ± 6.18, which correlates closely to the literature value.
Introduction
Sulfosalicylic acid is a triprotic acid whose structure is shown in figure 1. In water, the sulfonic acid group is completely deprotonated, and the phenolic group remains fully protonated unless the acid is subjected to very basic conditions. At a neutral pH, the carboxylic acid group is only partially deprotonated, and thus it can be shown that and equilibrium exists between a monoanion and a dianion, as shown in figure 2.
The equilibrium constant for this deprotonation can be calculated. Because the solvent (water in this case) is in great excess, an acid dissociation constant, Ka, can be defined, as in equation (1), where RH2– is the monoanion and RH2- is the dianion.
The value of Ka for this process has been found to be 2.13 x 10-3 mol dm-3 experimentally[1]. The dianion can act as a bidentate ligand, and forms highly coloured complexes with iron (iii) ions and displaces two water ligands, as in figure 3.
|
Figure 3 – monosubstitution of sulfosalicylic acid onto an iron (iii) ion |
Further substitution of the sulfosalicylic acid onto the iron ion may take place and form complexes such as FeR23- and FeR36-, however this only happens in largely alkaline conditions. The equilibrium constant for the monosubstitution reaction, β1, can be calculated using equation (2).
The equilibrium is pH dependant, and as pH is raised (the solution becomes more alkaline), the higher complexes with more than one sulfosalicylic acid ligand become stabilised at the expense of the lower complexes and the free iron (iii) ion. As a result, it can be assumed that only two iron containing species are present at any given pH. The experiment that was conducted was performed in fairly acidic conditions (pH 0 – 2.5), and so the predominating complex was the monosubstituted iron (iii) ion. Based on the assumption that only solvated and monosubstituted iron existed in the experiment, the total concentration of iron in the solution could be given by:
A similar assumption was made for the sulfosalicylic acid, in that the concentration of the acid in solution could be given by the sum of the concentrations of the unreacted acid, the dissociated acid and the acid bound to iron (iii) ions:
Because the complex is so highly coloured, then its concentration can be calculated by measuring the absorption at a wavelength that is only absorbed by the complex (determined to be 510 nm)[2].
Spectrophotometry is used widely in transition metal chemistry because many of the complex ions formed absorb light in the UV or visible region. The Beer-Lambert law (equation (5)) is an expression that can be used to determine the concentration of the complex from an absorbance reading, A, from a spectrophotometer if the molar absorption coefficient, ε, and path length, l, are known. Other applications of the Beer-Lambert law include the determination of the wavelengths that atmospheric gases, such as ozone, absorb light[3].
Combination and rearrangement of the Beer-Lambert law with the expressions for β1 and Ka give the following equation:
A plot of C1/A against G should be linear with an intercept of (ε1l)-1 and a gradient of (β1ε1l)-1, hence the graph can be used to determine molar extinction coefficient for the monosubstituted complex, ε1, and the stability constant for the first complexation, β1.
In the part of the experiment where the stoichiometry of the complex is determined, hydrochloric acid is used in each flask to fix the pH and ionic strength of the solutions.
In the part of the experiment where the stability constant for the first complexation is determined, hydrochloric acid is used to fix the pH of the Solution, and sodium nitrate was used to fix the ionic strength of the solutions.
The aims of this experiment were to determine, using the continuous variation method, the stoichiometry of the most predominant complex formed between iron (iii) and sulfosalicylic acid, and to determine the stability complex for its formation, β1, by using spectroscopic methods and plotting equation (6).
Experimental
Determination of the stoichiometry of the major complex formed
The eleven solutions detailed in table 1 were made up to 100 cm-3 with distilled water, and left to equilibrate for ten minutes. When the reagents were mixed, bright purple solutions were observed. The solutions in flasks 0 and 10 were essentially colourless compared to the other solutions. The intensity of the colour of the solutions increased from flask one to five, but decreased from flask five to nine.
|
Flask |
Volume of 0.5 M hydrochloric acid used / cm3 |
Volume of 0.05 M iron (iii) ammonium sulphate solution / cm3 |
Volume of 0.05 M sulfosalicylic acid solution / cm3 |
|
0 |
20 |
10 |
0 |
|
1 |
20 |
9 |
1 |
|
2 |
20 |
8 |
2 |
|
3 |
20 |
7 |
3 |
|
4 |
20 |
6 |
4 |
|
5 |
20 |
5 |
5 |
|
6 |
20 |
4 |
6 |
|
7 |
20 |
3 |
7 |
|
8 |
20 |
2 |
8 |
|
9 |
20 |
1 |
9 |
|
10 |
20 |
0 |
10 |
Table 1 – compositions of the solutions used to determine the stoichiometry of the complex formed
Absorbance was measured using a spectrophotometer set at 510 nm, and the results are quoted in appendix 1. These values were used to draw a job plot, which can be found in appendix 2. The stoichiometry of the complex was calculated to have a 1:1 ratio of iron (iii) to sulfosalicylic acid. The calculations used to determine this value are given in appendix 3.
Determination of the stability constant
The five solutions detailed in table 2 were made up to 50 cm3 with distilled water and left to equilibrate for fifteen minutes. A pH electrode was calibrated using a buffer solution of pH 2, and a buffer solution of pH 4. When the reagents were mixed, bright purple solutions were observed.
|
Flask |
Volume of 0.05 M sulfosalicylic acid / cm3 |
Volume of 0.005 M iron (iii) ammonium sulphate / cm3 |
Volume of 0.5 M hydrochloric acid / cm3 |
Volume of 4.0 M sodium nitrate / cm3 |
|
1 |
10 |
3 |
11 |
25 |
|
2 |
10 |
3 |
10 |
25 |
|
3 |
10 |
3 |
8 |
25 |
|
4 |
10 |
3 |
6 |
25 |
|
5 |
10 |
3 |
4 |
25 |
Table 2 – compositions of the solutions used to determine the stability constant of the complex
The solutions were all a bright purple colour, which increased in intensity from flask one to five. Measurements of absorption (using a spectrophotometer set at 510 nm) and pH were taken for each solution, and the results are listed in appendix 5. These values were used to draw a graph to determine the stability constant of the complex, which is shown in appendix 6.
Results and Discussion
Determination of the stoichiometry of the major complex formed
As shown in appendix 3, at the point at which the two lines on the job plot cross, their (x, y) coordinates are equal, and thus the equations can be solved simultaneously for x, the mole fraction of sulfosalicylic acid used. This was found to be 0.4981, and the expected value was 0.5, so the discrepancy of the experimental value was 0.26 %, however, the true nature of the experimental value can only be evaluated by calculating the propagated error due to the equipment used and apparatus used, the calculations for which can be found in appendix 4.
The absolute error for the absorbance reading for the solution in flask 5 is 1.483 ± 0.0426, which relates to 2.87 % of the experimental value. This value is small, and so does not invalidate the results of the experiment. It is unlikely any amount of the 2:1 complex was formed, because if this were the case, then the value of the mole fraction obtained would be much higher than 0.5. For 2:1 stoichiometry to occur, then the mole fraction of sulfosalicylic acid would be approximately 0.66.
If the experiment was repeated, it could be argued that using A-grade glassware would be beneficial in order to obtain more accurate results, however, since the error associated with the calculation was so small, it would be unnecessary.
Determination of the stability constant
Appendix 7 lays out the calculations necessary to determine the stability constant for the first complexation. The errors associated with this value are calculated in appendix 8. The value that was obtained for the stability constant was β1 = 420.45 ± 6.18
The error associated with this value is small, and so improving the accuracy of the glassware (using A grade instead of B grade glassware) would make little difference to the results of the experiment. The literature value for β1 is 480 ± 80[4], and the value obtained during the experiment falls within this range.
Conclusion
The aim of the experiment was firstly to determine the stoichiometry of the complex formed between iron (iii) and sulfosalicylic acid, and secondly to determine the stability constant, β1, for the formation of this complex.
It was found that there was a 1:1 ratio of iron (iii) to sulfosalicylic acid in the predominating complex because the mole fraction of iron was 0.502 when the most intensely coloured solutions were formed (indicating that a higher concentration of the complex was present in solution). The stability constant for the complexation was found to be β1 = 420.45 ± 6.18, which falls well within the range of the literature value. The accuracy of the values obtained was high since the magnitude of the errors associated with them were small, and are not significant enough to invalidate the results.
If the experiment was to be repeated, a different method could be used to acquire the information, for example, using methods such as NMR or mass spectrometry to determine the stoichiometry, or using potentiometric measurements in order to calculate the stability constant.
Further investigation could include investigation of the stability constants for higher complexes by increasing the pH of the reaction. It may be interesting to find the pH at which the predominating complex formed changes from a complex with one stoichiometry to another.
[1] E. Warminski, C. Crook, The Level 2 Chemistry Laboratory Manual, 2010 – 2011, Stability Constant page 2
[2] E. Warminski, C. Crook, The Level 2 Chemistry Laboratory Manual, 2010 – 2011, Stability Constant page 4
[3] L. Swanson, CHM2301 Lecture Course, University of Sheffield, 2010 – 2011
[4] A. Ågren, The complex formation between iron(III) ion and sulfosalicylic acid, Acta chemical scandinavica, 1954, 8, 279