Limiting Reactant
Written by Maxwell
Purpose: The purpose of this lab was to determine the formula of the product of the reaction between Barium Hydroxide (Ba(OH)2), and 4-Nitrophenol (C6H5NO3).
Procedure: For the outline of the procedure, please refer to pages 65-67 in the lab manual. However, part of the lab was specifically designed by the experimenter. Specifically, the method carried out in this lab was the Mole Ratio method. Subsequently, 100 mL of a 2.5 x 10-3 M solution of Ba(OH)2 was prepared by dissolving .0789 g of Ba(OH)2 in deionized water. To carry out the experiment, 4 mL of 2.5 x 10-3 M 4-Nitrophenol was added to 12 labeled test tubes. The solution of Ba(OH)2 was added in increasing increments of .5 mL from .5 mL to 6 mL. Water was then added to each test tube to reach a volume of 10 mL. Each of these mixtures was tested in a calibrated spectrophotometer.
Data/results:
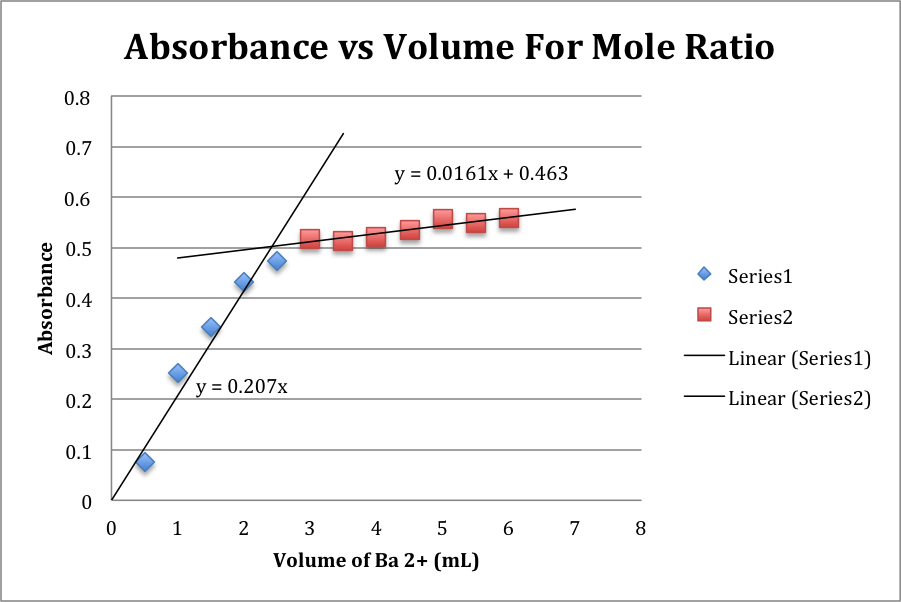
Chart of volume of Ba2+ solution used and the resulting absorbance of the final mixture.
| Volume of Ba2+ (mL) | Absorbance |
|
0.5 |
0.076 |
|
1 |
0.251 |
|
1.5 |
0.343 |
|
2 |
0.431 |
|
2.5 |
0.474 |
|
3 |
0.518 |
|
3.5 |
0.514 |
|
4 |
0.521 |
|
4.5 |
0.534 |
|
5 |
0.556 |
|
5.5 |
0.549 |
|
6 |
0.558 |
Graph of the preceding data, with trendlines (and their equations):
|
|
Coefficients |
Standard Error |
LCL |
UCL |
t Stat |
p-level | H0 (2%) rejected? |
|
Intercept |
0.29537 |
0.03716 |
0.19052 |
0.40022 |
7.94814 |
0.00002 |
Yes |
|
0.5 |
0.05195 |
0.00968 |
0.02464 |
0.07925 |
5.36833 |
0.00045 |
Yes |
Above is the linear regression information for the preceding graph.
The intersection point is at 2.42 mL
The Molar Ratio (n) is therefore 1.67
Calculations:
Intersection Point:
#mL Ni2+= (intercept2 – intercept1)/(slope2 – slope1)
2.42 mL = (0.463 – 0)/(0.207 – 0.0161)
n = (MC6H5NO3 x VC6H5NO3)/(MBa2+ x VBa2+)
1.67 = (2.5 x 10-3 M x .00400 L)/(2.5 x 10-3 M x .00242 L)
Discussion:
The volume of Ba(OH)2 solution added ranged from 0.5 mL to 6.0 mL. The absorbance that resulted ranged from .076 to .558. When plotted on the graph and with the resulting equations, it is seen that the intercept between these two lines is 2.42 mL. This signifies that the stoichiometric ratio of the two reactants is optimal at 2.42 mL of Ba(OH)2. Using this value to calculate the molar ratio of Ba(OH)2 to C6H5NO3, yields a value of 1.67. Since the barium ions react in a definite one mole ratio, we can assume that this n value becomes the subscript for the final product.
This poses a problem, because 1.67 does not fall near a whole number, which it would need to be in order to be a legitimate result. For the sake of discussion, 1.67 will be rounded to 2, in order to estimate the actual result. In fact, it turns out that the accepted value for “n” is indeed 2. There exists one main source of error in conducting this experiment. This is the inaccurate measurement of the volumes of solutions. A buret was used to dispense the appropriate amounts of each solution into the appropriate test tubes, and the inaccuracies of the starting and final volume of the buret when it comes to such small quantities were influential in the error experienced. One other source of error was the personal judgment used in creating the trendlines on the observed graph. Since the start of the second trendline cannot be identified with perfect accuracy, the intersection point (and subsequently the n value) consequently may differ.
Conclusion:
The purpose of this experiment, to find the formula structure of the products of the reaction between Barium Hydroxide (Ba(OH)2), and 4-Nitrophenol (C6H5NO3), was partly successful. The n value achieved was not entirely accurate, however, upon rounding, it yielded the appropriate result.