Formation of Microtornadoes, Microgeysers, and Liesegang Banding Patterns from HCl-NH3 Nanoparticulate, Topochemically Arranged Experimental Systems
Formation of Microtornadoes, Microgeysers, and Liesegang Banding Patterns from HCl-NH3 Nanoparticulate, Topochemically Arranged Experimental Systems
Abstract:
In this report, we will analyze the mechanisms by which various micro-structures form, from diffusion to the formation of a reaction front and to convection. The nucleation to growth theory will also be discussed using the HCl-NH3 nanoparticulate experimental system to better understand how aerosols chemically function in the atmosphere. The experiments outlined in a series of papers published by Dr. Stephen Thompson and Dr. Patrick Shipman were carried out in glass and plastic containers of different shapes and sizes to allow diffusion of both gases to occur. One set of counter-diffusional experiments describes how the diffusion of both gases on opposite ends of a glass tube (one type of reaction chamber) form a reaction front made of NH4Cl(s). As the reaction front moves down the tube, Liesegang rings begin to form via rates of heterogeneous and homogeneous nucleation and growth. Discussion of how the pattern formations vary will be covered in this report as well. The second set of experiments were carried out in petri dishes where microtornadoes and microhurricanes formed because the hemispherical zones of the petri dishes affected the vapors to form “tornadic” structures that streamed downward from the top to the bottom of the petri dish, forming tubes of aerosol. The third set of experiments formed microgeysers as a result of how the chemical solutions were topochemically position in the reaction chamber. The publications describe how these various container experiments were set up and how the results changed depending on the differences in diffusion coefficients, differences in the concentration of reactants, differences in vapor pressures, temperatures, and different ways of setting up the experiments. Suggested thermodynamic and kinetic analyses of the HCl- NH3 reaction are examined in the report as well. Overall, the main goal of these nano-scale chemistry experiments was to create small-scale analogs to study how and by what mechanisms aerosols form to obtain insight on the nature of pattern formation which plays a big role in climate behavior. One, potential, long-term goal from these experiments is to prevent air pollution by controlling the generation of aerosols.
Background Chemistry:
Aerosols
Aerosols are very small particles in the air that are made from atmospheric bases and acids in our atmosphere. Because they can range from .01 to 1 micron (μm), their surface area is very big while their volume is small. Since there are over 100,000 aerosols per cubic centimeter, aerosols contribute a lot to atmospheric visibility. Their surface area attracts many chemical pollutants that highjack on aerosols while creating chemical reactions that cause visibility degradation that cover a wide variety of aerial dispersions. (Aerosol Science, Davies) Aerosols are also important in the formation of clouds, light scattering, and climate forcing. Some properties of aerosols include their ability to move with the flow of air stream and having long resistance times depending on their size. It is important to note that the bigger an aerosol is, the faster it settles. Aerosol science is imperative in atmospheric processes, global warming and cooling, in air pollution control technology and in the medical field. (Aerosol Science, Davies) If we can understand the mechanisms by which the aerosols form, we can potentially develop techniques in controlling air particulate concentrations in the atmosphere and battle with the health effects caused by the toxins on the surfaces of those aerosols that get inhaled. (Aerosol Science, Davies)
Air Pollution and Global Warming
Every day, we breathe in approximately 20,000 liters of air into our lungs. But every breath we take has millions of aerosols that may carry dangerous chemicals which have escaped into the atmosphere from fossil fuel combustion reactions. Combustion of fossil fuels produces millions of nanoparticulate soot, that indirectly form atmospheric aerosols such as ammonium sulfate, ammonium nitrate and ammonium chloride.(Elsevier, Thompson) Air pollution occurs because it has contaminants traveling in the atmosphere, causing negative effects to our society, our health and our ecosystems. These substances that are termed “air pollutants” are either in the form of gases or nano-particles which allows them to have a very long resistance time in the air. Long resistance time allows these particles to move for long periods of time and cover great distances, transporting air toxins from one place to another. In short, these pollutants are everywhere.
The combustion of fossil fuels that are mostly made up of hydrocarbons contributes greatly to air pollution. Small amounts of nitrogen and sulfur are also present. (Chemtrek, Thompson) Other factors that contribute to air pollution are industrial use of chemicals and production of automobiles. In a sense, these sources of air pollution are anthropogenic and human activity of producing energy sources has essentially created Global Warming. In a way, Global Warming can be seen as pure evidence that our atmosphere is highly sensitive to man-made deposition upon increasing the nitric cycle by 50%, carbon by 20%, and sulfur cycle by 100%. (Chemtrek, Thompson)
Where do all of these pollutants come from?
- Nitrogen compounds
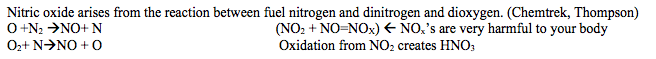
- Sulfur compounds:
Combustion of coal creates a lot of the sulfur emissions out in the atmosphere.
SO2 oxidizes into SO3 when it combines with H2O2, and when SO3 comes together with H2O, we have H2SO4. The combination of SO2 and SO3 creates SOx’s. (Chemtrek, Thompson)
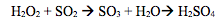
- Hydrocarbons:
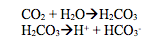
Carbon dioxide reacts with water to form carbonic acid and then this acid dissociates to give a hydrogen ion and the hydrogen carbonate ion.
Why should we care?
Global Warming has increased the average temperature of the Earth’s surface, the atmosphere, and of the oceans. Greenhouse gases such as, CO2, CH4, and N2O are mostly responsible for such a dramatic increase in temperature over the last 2 centuries. The greenhouse gases produced from all of these chemical reactions are absorbed by the Earth’s soil, they go into our oceans, they go up into the atmosphere, and they’re inhaled by our lungs and pass down to our blood stream. In the atmosphere, we’re fighting with air pollution. In our bodies, we’re battling with the toxins we’ve inhaled. In the oceans, coral reefs are being destroyed and the pH is becoming more and more acidic. On Earth, as the soil absorbs all of the toxins and acid deposition, it begins to have a buildup of SO4. Acid deposition causes environmental damage. Ultimately, the environmental impact of acid deposition changes the weather. We should care because if we do not come up with solutions on how to prevent so many of these toxins from going up into the atmosphere, then they will just keep on harming us. These toxins affect natural oxidation and respiration. Without photosynthesis and respiration, our lives cease to exist! (Chemtrek, Thompson) It is essential to understand the mechanisms by which aerosols form.
Introduction:
Dr. Stephen Thompson’s and Dr. Patrick Shipman’s publication titled: Patterns, Oscillations, and Microtornadoes: Extreme Events in Vapor to Particle Reaction Zones outline mechanisms of different vapor to particle, acid-base, proton-transfer reactions in different types of containers to analyze nucleation, growth, aggregation, charging processes and oscillatory behavior in the reaction zones to gain insight on how aerosols behave in the atmosphere. For simplicity, this report will only focus on one type of acid-base reaction that occurs in our atmosphere and that is the HCl and NH3 reaction. As the two gases react in a given container, solid ammonium chloride particles form and a reaction front is established, followed by either the formation of Liesegang bands, generation of microtornadoes, or microgeysers. The modes by which the ammonium chloride particulates form depend on the topochemistry of the reaction. Light scattering sources were used to focus on the formation of the reaction front. Theories of how the patterns of Liesegang bands and the microstructures were proposed and mathematical modeling on the patterns and behavior of the reactions were also done.
Materials and Methods:
All of the reactions were carried out in either transparent, polystyrene glass containers or glass tubes. Particle formation and reaction zones were identified by various light scattering sources such as lasers. Reactants were topochemically positioned in order to track the reaction location. The reaction zones were controlled by vapor concentrations of the reactants and all of the vapors were produced from the aqueous solutions of the reagents. The temperature was 25°C. Light sources with low voltages were used for light scattering methods.
Experimentation and Results:
Micro-Liesegang Rings and the Counter-Diffusional Tube Experiments
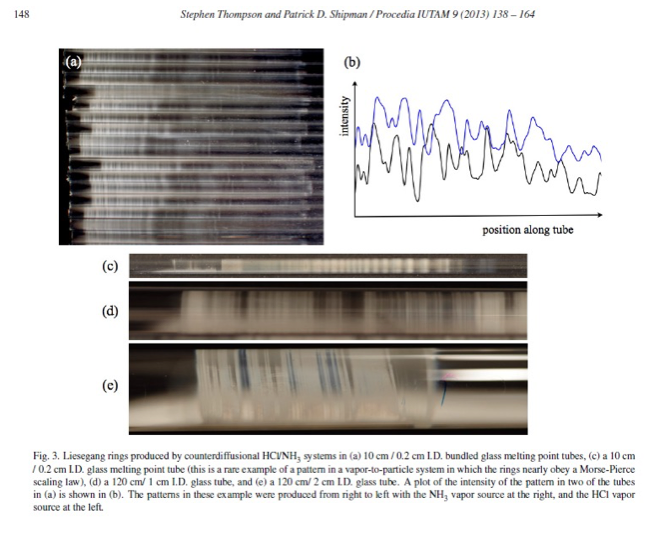
A polystyrene glass tube was positioned horizontally via clamps above a bench top. Aqueous solutions of varying concentration of NH3 and HCl were pipetted into plugs of fiberglass wool. The plugs were placed into hollow polyethylene caps that were inserted into the opposite ends of the glass tube, simultaneously. The lights in the room were turned off. As the gases began to diffuse, both He and Ne lasers were swept continuously throughout the tube to spot the formation of a reaction front. After crystal faces of the first aerosols appeared, wall nucleation began to occur. Upon wall nucleation, a reaction front was established, followed by the formation of the first Liesegang band. After the first band of precipitate was formed, there was a precipitate free zone, followed by a second Liesegang band. These band formations continued to form for the next several hours. These counter-diffusional reactions can last as much as several days, forming concentric bands or spirals inside the tube. The direction in which the rings form can either go towards HCl or NH3 based on the concentration of the molar solutions. If the experiments are set up in rectangular tubes, we get Liesegang squares. So, overall, the shape of the reaction-container affects the formation of Liesegang precipitates. (Elsevier, Thompson)
Microtornadoes
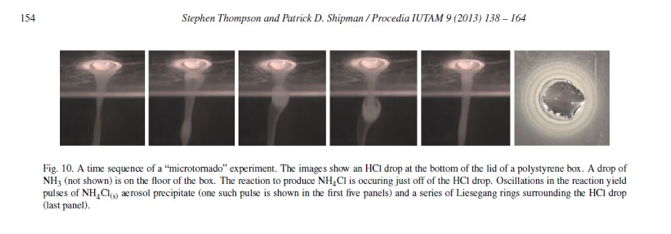
One drop of 6M NH3 on the bottom-half of a Petri dish was placed and one drop of 6M HCl was placed directly above the ammonia drop on the top-half of the Petri dish. Thin aerosol smoke formed in the dish and a reaction front was established <.1cm away from the drop of HCl. Ammonium chloride particulates formed and they slid down in a turbulent stream towards the NH3 drop. As the particulates dropped down, tubes of aerosol were formed and fell to the bottom, leaving a ring of deposit at the surface, around the NH3 drop. Tornado direction can be reversed by changing the HCl-NH3 concentrations. (Elsevier, Thompson)
Microgeysers
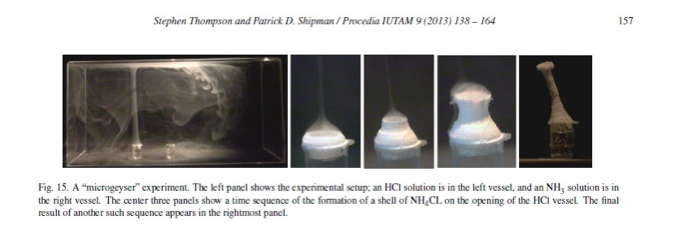
Aqueous solutions of 14.8M NH3 and 11.8M HCl were placed in wells, separated 3cm apart and placed into a box shaped, polystyrene container. The NH4Cl smoke shot upward from the NH3 well and the build-up of precipitate grew around the well containing the HCl solution. As the precipitate piled up, the aerosol closed the opening of the well. Here, it was observed that the reaction was emitting heat energy because the solutions had cooled at the end of the reactions. (Elsevier, Thompson)
Discussion:
The special structures are determined by the modes in which the precursor gases are brought together. All of the reactions have defined reaction zones where fast kinetics, interaction of the movement of vapors and charge redistribution produce various morphologies of the ammonium chloride salts. Microtornadoes and microhurricanes form because the vapors of HCl and NH3 react in the hemispherical zone of the petri dish to give nanoparticulate NH4Cl(s) that streams downward in the form of rotating tubes. Microgeysers form because of how the solutions of HCl and NH3 were topochemically set up in the apparatus (next to each other) and because of their very strong concentrations. Band patterns formed because of the rates of heterogeneous and homogeneous nucleation and growth that directly affected the moving zone by slowing it down and then resuming again. Although the gravitational, convectional and charging forces govern the reactions, the nucleation to growth process is the foundation for how ammonium chloride salts form. The Nucleation to Growth theory is discussed below along with the proposed mechanism of the Kinetics and Thermodynamics of the HCl-NH3 reaction.
Kinetics Analysis
The publication proposed a step-by-step mechanism for the HCl-NH3 reaction. It is outlined below:

Water particles and Cl– ions are catalysts in the reaction. Charge redistribution occurs before the addition of HCl and NH3 can occur. Macroscopic ammonium chloride particles form because of the growth of the critical cluster proceeds. (Elsevier, Thompson)
Thermodynamic Analysis
It is suggested that the thermodynamic driving force for the reaction is the lattice energy released in the cumulative combination of NH4+(g) + Cl–(g)àNH4Cl(s) The entropy change for the reaction was calculated to be -285.2J mol-1K-1 and the enthalpy change was -176.4kJ mol-1 and the standard free energy change is -91.4kJ mol-1. The reaction is spontaneous. (Elsevier, Thompson)
Nucleation and Growth of HCl-NH3 Reaction using Tubes Forming Liesegang Rings as an Example:
To begin, the natural processes of cloud formation have an inherent mechanism involving nucleation and growth in the phase transition of vapors of two different gases that generate a substantial amount of air particulates upon reacting together. The phase transition here is caused by supersaturation where gaseous molecules of two separate compounds form solid particles of a new compound. One of the glass containers used to demonstrate this reaction was done in an open-ended glass tube, where one end was capped with a wool glass ball soaked with HCl liquid and the other end was capped with NH3 liquid. The gases of these two separate liquids began to counter diffuse and once they reacted, a reaction front was formed that moved down the tube creating Liesegang bands. Heterogeneous nucleation occurs before the unstable clusters of NH4Cl(s) reach a critical point upon which the energy barrier to homogeneous nucleation can occur. Once homogenous nucleation begins the rate of nucleation increases so that the molecules begin to nucleate with other molecules and once a critical threshold is achieved, growth of clusters via aggregation occurs and a reaction front is then established in the tube. A figure of this process is shown below. Formation of clusters of a new phase (solid state) requires energy to create a surface meaning that there is an energy barrier to nucleation. This is why the first clusters of the salt are unstable. The clusters are stable because of the bulk molecules but they are unstable because of the surface molecules and as the concentration of molecules increases, stability of the clusters allows them to eventually overcome the energy barrier. Post-nucleation growth takes place via aggregation and that is why we can see ammonium chloride bands form in the tube. The reason Liesegang bands form is because the reaction has differences in diffusion coefficients and differences in concentration of reactants. More specifically, those differences make the reaction front move down the tube and the nucleation to growth process is continuous and that creates bands of precipitate along the tube with precipitate free zones in between the bands. The modes by which the precursor gases come together determine the special structures of the bands in the tube.
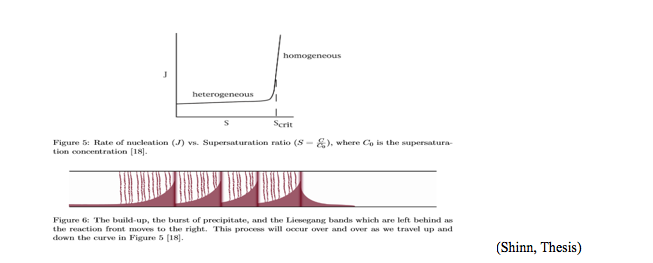
In short, all of these reactions have electron-transfer, nucleation, growth and charging processes that govern the generation of aerosols.
Publications/References:
- Thompson, Stephen, and Patrick Shipman. “Patterns, Oscillations, and Microtornadoes: Extreme Events in Vapor-to-particle Reaction Zones.” Elsevier 9 (2013): 138-64. Print.
- Shinn, Jamie. “NUCLEATION AND GROWTH: MODELING THE NH 3 – HCL REACTION.” Colorado State University, 2012. Print.
- Thompson, Stephen, and Patrick Shipman. “Topochemical Diffusion-reaction-convection Dynamics in Vapor-to-particle Aerosol Nucleation and Growth.” AIP Conference Proceedings (2013): n. pag. Web.
- Thompson, Stephen. Chemtrek: Small-scale Experiments for General Chemistry. Boston: Allyn and Bacon, 1990. Print.
- Davies, C. N. Aerosol Science,. London, NY: Academic, 1966. Print.
